三种上采样方式总结

在GAN，图像分割等等的网络中上采样是必不可少的。这里记录一下自己学到的三种上采样方式：反卷积(转置卷积)，双线性插值+卷积，反池化。

反卷积(转置卷积)

卷积只会减小或不变输入的大小，转置卷积则是用来增大输入的大小。用于细化粗的特征图等等，FCN中就有应用。这里一个图就能很简单表明他做的事情。感觉就是做的卷积反过来的事情。转置卷积是可以进行学习的。

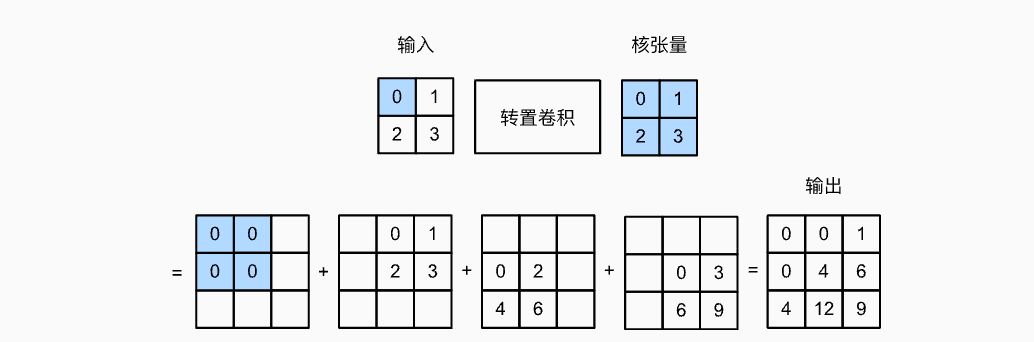
kernel核张量与输入的张量中，逐个元素相乘，放在对应的地方。就是说第一个元素是0，就是0乘上整个核张量，放在对应的位置。第二个元素是1则是乘上核张量放在对应滑动到下一个位置。以此类推。得到四个图，将四个图相加即可得出最终输出。此处的例子stride为1，所以滑动的步长是1。

总结出来的公式为：

其中Y的大小就是卷积的大小计算公式反过来：

卷积： out = (Input - kernel + 2*padding) / stride + 1

反卷积： out = (Input - 1) stride + kernel - 2padding

Stride就是核的滑动步长，这个很好理解

padding：这里的padding和卷积不同，卷积是外边加一圈0。转置卷积则是给输出部分减掉一圈作为输出。

称为转置的原因：

对于卷积Y = X ⊙ W，将Y，X分别展开成一个向量，Y’，X’表示。W等价于一个V使得

转置卷积等价于详细的网上很多博客也写过。轻松理解转置卷积

手写实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

import torch

def trans_conv(X, K):
    h, w = K.shape
    Y = torch.zeros((X.shape[0] + h - 1, X.shape[1] + w - 1))
    for i in range(X.shape[0]):
        for j in range(X.shape[1]):
            Y[i:i+h, j:j+w] += X[i, j] * K
    return Y
# 手写计算
X = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
print(trans_conv(X,K))

# torch的ConvTranspose2d
X, K = X.reshape(1, 1, 2, 2), K.reshape(1, 1, 2, 2)
tconv = torch.nn.ConvTranspose2d(1, 1, kernel_size=2, bias=False)
tconv.weight.data = K
print(tconv(X))

out：

tensor([[ 0., 0., 1.],
[ 0., 4., 6.],
[ 4., 12., 9.]])
tensor([[[[ 0., 0., 1.],
[ 0., 4., 6.],
[ 4., 12., 9.]]]], grad_fn=< SlowConvTranspose2DBackward>)

两个输出是一样的。

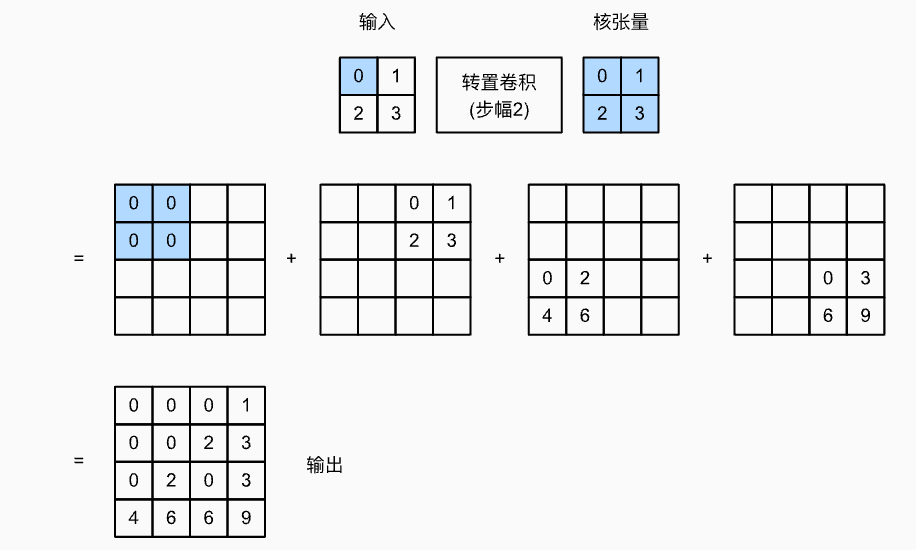
加上stride设置

1
2
3
4
5
6
7
8
9

...
def trans_conv(X, K, stride=1):
    h, w = K.shape
    Y = torch.zeros(((X.shape[0] - 1) * stride + h, (X.shape[1] - 1) * stride + w))
    for i in range(X.shape[0]):
        for j in range(X.shape[1]):
            Y[i * stride:i * stride +h, j * stride:j * stride +w] += X[i, j] * K
    return Y
...

将对应ConvTransposed2d中设置stride为2，trans_conv()中的stride设为2

out:

tensor([[0., 0., 0., 1.],
[0., 0., 2., 3.],
[0., 2., 0., 3.],
[4., 6., 6., 9.]])
tensor([[[[0., 0., 0., 1.],
[0., 0., 2., 3.],
[0., 2., 0., 3.],
[4., 6., 6., 9.]]]], grad_fn=< SlowConvTranspose2DBackward>)

padding设置为1，stride设置为1，可以得出

out：

tensor([[[[4.]]]], grad_fn=< SlowConvTranspose2DBackward>)

双线性插值+卷积

前面转置卷积虽然可以将图扩大尺寸，细化粗特征图。但是存在一个棋盘效应问题。

棋盘效应：转置卷积不均匀重叠导致的，使得图像变得有棋盘格一样的像素块

解决办法是使用双线性插值先将图片扩大，在用卷积即可。下面先介绍单线性插值然后再是双线性插值。

单线性插值

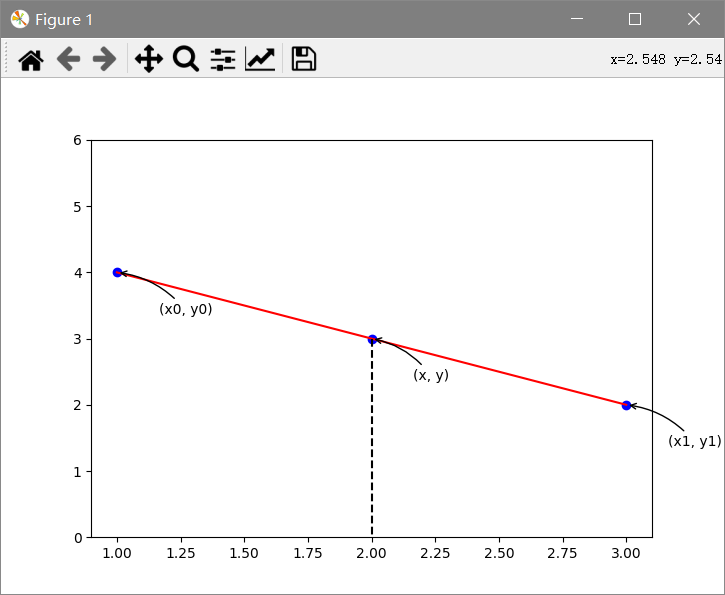
很简单，可以说高中生都能搞定。给出两点，算出方程，然后求中间任一点y。公式如下

然后将对应的y值插入即可。

双线性插值

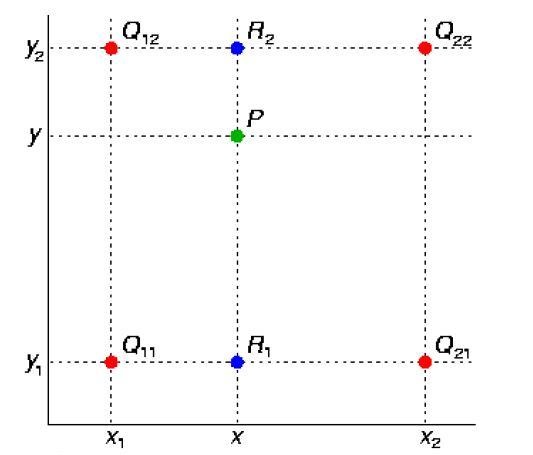
如图通过已知的四个点Q11，Q12，Q21，Q22求得中间P(x, y)点的值。现在x方向进行线性插值得到R1和R2，再在y方向上做线性插值得到f(x, y)求得P点。

公式如下

x方向求R1，R2

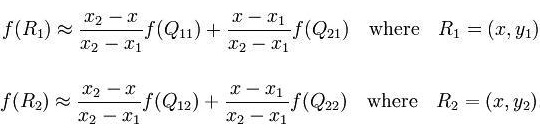
y方向求P

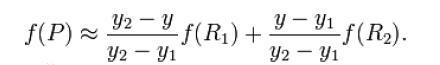
扩大之后在进行卷积，完成上采样

代码

1
2
3
4
5
6
7
8
9

import torch.nn as nn
...
upsample_bil = nn.UpsamplingBilinear2d(scale_factor=2)
# or
net = nn.Upsample(scale_factor=2, mode='bilinear', align_corners=True)
# or
F.interpolate(input, size, scale_factor, mode, align_corners)
...
# 都有size参数，可以指定放大的大小。scale_factor指定放大倍数。mode指定放大模式

反池化

最开始看到反池化的论文是在DeConvolution Network和SegNet当中，这两个网络是相当的相似。这里只说反池化(Unpooling)

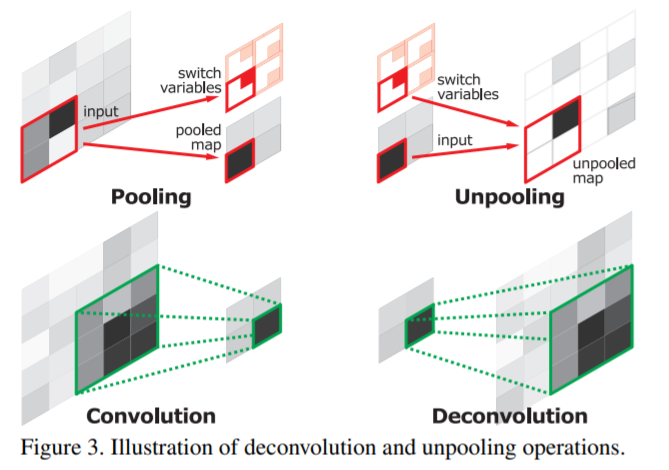
简单来说，就是在下采样的过程中，maxpool的时候记录一个池化的索引，就是记录取得的这个值是在那个位置。在反池化的时候，输入的值根据索引放回原来的位置，得到一个稀疏矩阵。然后通过后边的卷积层（DeconvNet是用的转置卷积，SegNet用的卷积）学习将粗的特征图进行细化。这种反池化的操作，索引记录了更多的边缘信息，可以加强刻画物体的能力，通过重用这些边缘信息，加强精确的边界位置信息。在分割的时候有助于产生更平滑的分割。

使用代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14

test = torch.rand((2, 3, 128, 128))
print("Original Size -> ", test.size())
# maxPool池化
maxpool = nn.MaxPool2d(2, 2)
# 设定要返回索引
maxpool.return_indices = True
# 记录池化结果，索引结果
mp, indices = maxpool(test)
print("MaxPool -> ", mp.size())
# 设置MaxUnpool反池化
unpooling = nn.MaxUnpool2d((2, 2), stride=2)
# 传入参数和索引
upsamle = unpooling(mp, indices)
print("MaxUnpool -> ", upsamle.size())

out:

Original Size -> torch.Size([2, 3, 128, 128])
MaxPool -> torch.Size([2, 3, 64, 64])
MaxUnpool -> torch.Size([2, 3, 128, 128])

参考资料

转置卷积【动手学深度学习v2】

动手学深度学习

双线性插值-百度百科