本文最后编辑于 前,其中的内容可能需要更新。
1104. 二叉树寻路
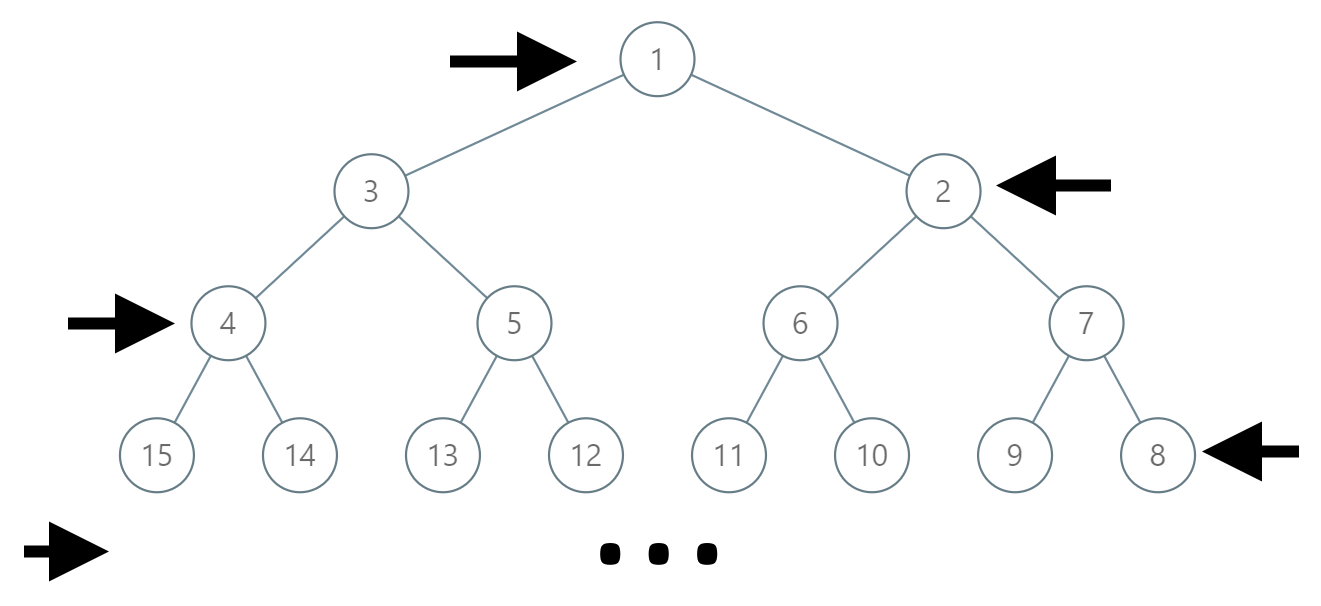
在一棵无限的二叉树上,每个节点都有两个子节点,树中的节点 逐行 依次按 “之” 字形进行标记。
如下图所示,在奇数行(即,第一行、第三行、第五行……)中,按从左到右的顺序进行标记;
而偶数行(即,第二行、第四行、第六行……)中,按从右到左的顺序进行标记。
原文地址
给你树上某一个节点的标号 label,请你返回从根节点到该标号为 label 节点的路径,该路径是由途经的节点标号所组成的。
示例 1:
1
2
| 输入:label = 14
输出:[1,3,4,14]
|
示例 2:
1
2
| 输入:label = 26
输出:[1,2,6,10,26]
|
提示:
解题思路
利用公式,计算高度。
其中
m: m叉树
n: n个节点
二叉树当中,每个节点整除之后就是父亲节点。奇数层是顺序,偶数层是逆序,我的做法是,假设都是顺序,那么我可以找到一个顺序形式下的路径,通过2^(floor - 1)和2^(floor) - 1,可以知道当前层最大最小值,根据算出的父亲节点值,知道相对位置,在根据奇偶层,相应更改对应位置的值是顺序的第几个或者逆序的第几个,但是我计算用的值不变。然后数组就用前插就能完成根节点到对应label位置
解题代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| public class algorithm1104 {
@Test
public void test(){
List<Integer> list = pathInZigZagTree(26);
for (Integer item:list) {
System.out.println(item);
}
}
public List<Integer> pathInZigZagTree(int label) {
List<Integer> list = new LinkedList<>();
double high = Math.log((label + 1)) / Math.log(2);
int ceil = (int) Math.ceil(high);
int point = label;
list.add(label);
if((ceil & 1) == 0){
int max = (1 << ceil) - 1;
int min = (1 << (ceil - 1));
point = (min + max - point);
}
while(point > 1){
point = point >> 1;
ceil--;
if((ceil & 1) == 1){
list.add(0,point);
}else{
int max = (1 << ceil) - 1;
int min = (1 << (ceil - 1));
list.add(0,(min + max - point));
}
}
return list;
}
}
|
