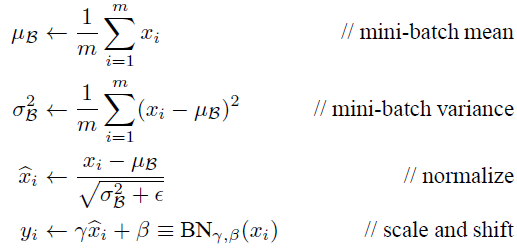菠萝菠萝卜的博客

深度学习入门笔记06

  • 2021-09-30
  • 作者 菠萝菠萝卜
  • ~6.63K 字
  • 次阅读
  1. 1. 参数更新
    1. 1.1. SGD
      1. 1.1.1. SGD缺点
    2. 1.2. Momentum
    3. 1.3. AdaGrad
    4. 1.4. Adm
  2. 2. 权重的初始值
    1. 2.1. 隐藏层的激活值的分布
    2. 2.2. ReLu初始值
  3. 3. Batch Normalization

参数更新

这里就是将之前的权重更新的算法，封装成一个类。每个类里面都有一个update方法，这样往后如果需要修改更新权重的方法（SGD，Momentum，AdaGrad，Adm），直接更改对应类的对象即可。

e.g

1
2
3
4
5
6
7
8
network = TwoLayersNet(...)
optimizer = SGD() #此处可以更换更新方法
...
for i in range(50000):
    ...
    grads = network.gradient(x_batch,y_batch)
    params = network.params
    optimizer.update(params,grads)

SGD

随机梯度下降法，和之前一样，这里只是做了封装

python实现

1
2
3
4
5
6
7
8
import numpy as np
#随机梯度下降法
class SGD:
    def __init__(self,lr = 0.01):
        self.lr = lr
    def update(self,params,grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key]

SGD缺点

SGD的下降方式呈现“之”字形，比较低效。

Momentum

数学表达：

此处的v相当于物理中的速度，α模拟的阻力。这种方法会更快的向x轴靠近，减少之字形带来的影响。

AdaGrad

学习率衰减法：随着学习进行，学习率逐渐变小，开始多学，后面少学。

数学公式：

新变量h，它保存了以前所有梯度值的平方和，更新参数时，通过乘以1除根号h，调整学习尺度。参数的元素中变动较大的元素的学习率将变小。

python实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#学习率衰减
class AdaGrad:
    def __init__(self,lr = 0.01):
        self.lr = lr
        self.h = None
    def update(self,params,grads):
        if self.h is None:
            self.h = {}
            for key,val in params.items():
                self.h[key] = np.zeros_like(val)

        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)

Adm

这里具体原理没有详讲，只是贴下代码

python实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Adam:

    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
        self.lr = lr
        self.beta1 = beta1
        self.beta2 = beta2
        self.iter = 0
        self.m = None
        self.v = None
        
    def update(self, params, grads):
        if self.m is None:
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)
        
        self.iter += 1
        lr_t  = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)         
        
        for key in params.keys():
            #self.m[key] = self.beta1*self.m[key] + (1-self.beta1)*grads[key]
            #self.v[key] = self.beta2*self.v[key] + (1-self.beta2)*(grads[key]**2)
            self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
            self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
            
            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
            
            #unbias_m += (1 - self.beta1) * (grads[key] - self.m[key]) # correct bias
            #unbisa_b += (1 - self.beta2) * (grads[key]*grads[key] - self.v[key]) # correct bias
            #params[key] += self.lr * unbias_m / (np.sqrt(unbisa_b) + 1e-7)

权重的初始值

权重的初始值设定很重要，这个会导致学习是否会快速进行

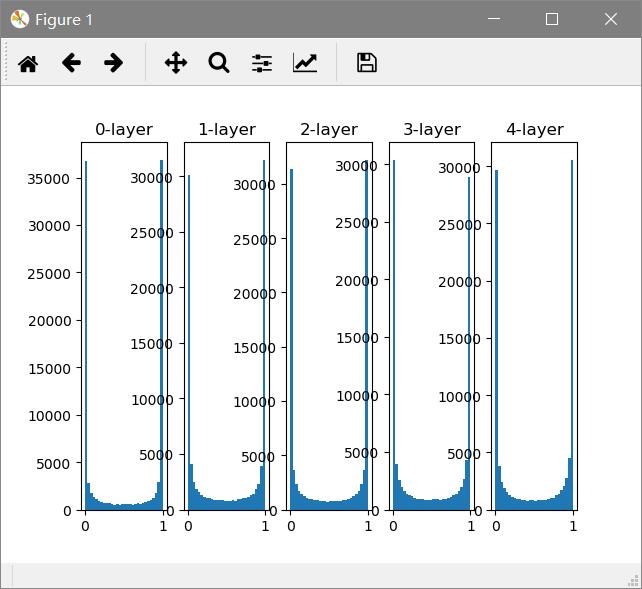
隐藏层的激活值的分布

假设这里有5层神经网络，激活函数使用sigmoid，传入随机数据，观察分布。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
    return 1 / (1 + np.exp(-x))
def ReLu(x):
    m = (x <= 0)
    x[m] = 0
    return x

x = np.random.randn(1000,100) #1000个数据
node_num = 100      #各个隐藏层的节点数量
hidden_layer_size = 5 #5个隐藏层
activations = {}    #激活值的结果保存在这里

for i in range(hidden_layer_size):
    if i != 0:
        x = activations[i - 1]

    w = np.random.randn(node_num, node_num) * 1
    z = np.dot(x,w)
    a = ReLu(z)
    activations[i] = a
#绘图
for i, a in activations.items():
    plt.subplot(1,len(activations),i+1)
    plt.title(str(i) + "-layer")
    plt.hist(a.flatten(), 30 , range=(0,1))
plt.show()

out:

这个代码中主要关注的是权重的尺度，标准差的选择。从图中看，由于是sigmoid函数，随着输出不断靠近0或1，他的导数值逐渐接近0，因此偏向0和1的数据分布会造成反向传播中梯度的值不断变小，最后消失。这个问题就是梯度消失。层次加深的深度学习中，梯度消失问题会更加严重。

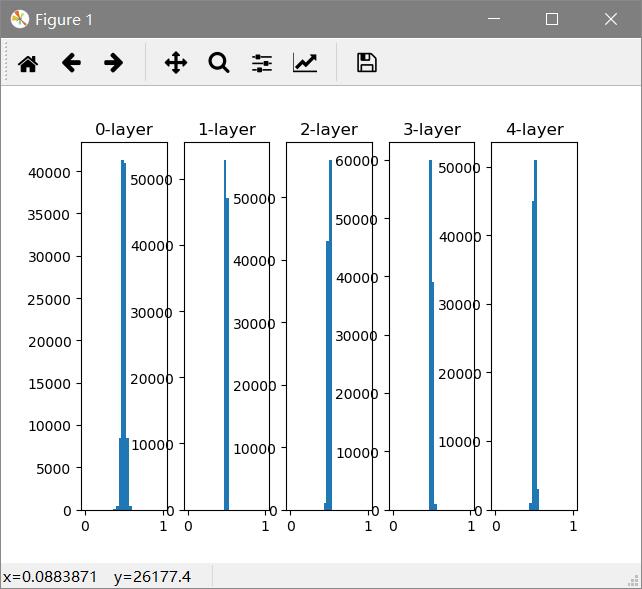
将标准差变为0.01后

1
w = np.random.randn(node_num, node_num) * 0.01

out:

这次呈现集中在0.5分布，不会发生梯度消失问题。激活值的分布有所偏向，在表现力上会有问题，多个神经元输出几乎相同的值，那他们也没有存在的意义了。

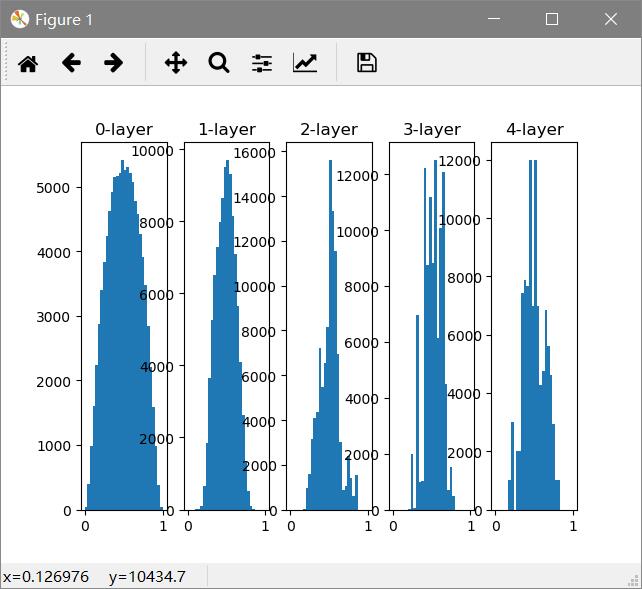
尝试Xavier Glorot推荐的权重初始值:

如果前一层的节点数为n，则初始值使用标准差为1/√n 的分布

从结果可知，越是后面的层，图像变得更歪斜，呈现了比之前更有的广度分布。因为各层间传递的数据有适当的广度，sigmoid表现力不受限制。

ReLu初始值

推荐Kaiming He初始值，也称为“He初始值”，使用标准差为√(2/n)的高斯分布。

Batch Normalization

使用Batch Normalization，使得各层拥有适当的广度，“强制性”的调整各层的激活值分布。

优点：

  • 使得学习更加快速进行

  • 不那么依赖初始值

  • 抑制过拟合

为了有适当的广度，所以需要在神经网络中添加正规化层，就是Batch Normalization层。

BN层做的事情就是使得数据分布为0、方差为1的正规化。过程如下

这里ε是一个极小值，防止下边变为0导致计算错误。

此处γ的值初始值为1，β值为0，后续通过学习调整到合适的值。

python实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
class BatchNormalization:
    """
    http://arxiv.org/abs/1502.03167
    """
    def __init__(self, gamma, beta, momentum=0.9, running_mean=None, running_var=None):
        self.gamma = gamma
        self.beta = beta
        self.momentum = momentum
        self.input_shape = None # Conv层的情况下为4维，全连接层的情况下为2维  

        # 测试时使用的平均值和方差
        self.running_mean = running_mean
        self.running_var = running_var  
        
        # backward时使用的中间数据
        self.batch_size = None
        self.xc = None
        self.std = None
        self.dgamma = None
        self.dbeta = None

    def forward(self, x, train_flg=True):
        self.input_shape = x.shape
        if x.ndim != 2:
            N, C, H, W = x.shape
            x = x.reshape(N, -1)

        out = self.__forward(x, train_flg)
        
        return out.reshape(*self.input_shape)
            
    def __forward(self, x, train_flg):
        if self.running_mean is None:
            N, D = x.shape
            self.running_mean = np.zeros(D)
            self.running_var = np.zeros(D)
                        
        if train_flg:
            mu = x.mean(axis=0)
            xc = x - mu
            var = np.mean(xc**2, axis=0)
            std = np.sqrt(var + 10e-7)
            xn = xc / std
            
            self.batch_size = x.shape[0]
            self.xc = xc
            self.xn = xn
            self.std = std
            self.running_mean = self.momentum * self.running_mean + (1-self.momentum) * mu
            self.running_var = self.momentum * self.running_var + (1-self.momentum) * var            
        else:
            xc = x - self.running_mean
            xn = xc / ((np.sqrt(self.running_var + 10e-7)))
            
        out = self.gamma * xn + self.beta 
        return out

    def backward(self, dout):
        if dout.ndim != 2:
            N, C, H, W = dout.shape
            dout = dout.reshape(N, -1)

        dx = self.__backward(dout)

        dx = dx.reshape(*self.input_shape)
        return dx

    def __backward(self, dout):
        dbeta = dout.sum(axis=0)
        dgamma = np.sum(self.xn * dout, axis=0)
        dxn = self.gamma * dout
        dxc = dxn / self.std
        dstd = -np.sum((dxn * self.xc) / (self.std * self.std), axis=0)
        dvar = 0.5 * dstd / self.std
        dxc += (2.0 / self.batch_size) * self.xc * dvar
        dmu = np.sum(dxc, axis=0)
        dx = dxc - dmu / self.batch_size
        
        self.dgamma = dgamma
        self.dbeta = dbeta
        
        return dx
本作品采用 知识共享署名-相同方式共享 4.0 国际许可协议 进行许可
, ,
最后编辑：2022-05-03