菠萝菠萝卜的博客

深度学习入门笔记05

  • 2021-09-28
  • 作者 菠萝菠萝卜
  • ~4.00K 字
  • 次阅读
  1. 1. 误差反向传播法
    1. 1.1. 计算图
    2. 1.2. 局部计算
    3. 1.3. 为何用计算图解题
    4. 1.4. 计算图的反向传播
  2. 2. 反向传播
    1. 2.1. 加法节点的反向传播
    2. 2.2. 乘法节点的反向传播
    3. 2.3. 回到苹果的例子
  3. 3. 激活函数层实现
    1. 3.1. ReLU层
    2. 3.2. sigmoid层
    3. 3.3. Affine/Softmax 层

误差反向传播法

计算图

计算图：将计算过程用图形表达出来。

首先说下书上的例子：

问题1：太郎在超市买了2个100日元一个的苹果，消费税是10%，请计算支付金额。

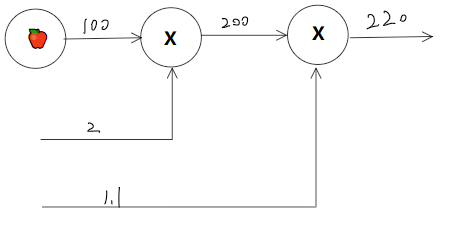
相当简单的一道题， 2 100 1.1即可。计算图表示则是：

将x2和x1.1节点中的数字取出，符号单独放在○当中。

这种从左往右的计算方式为正向传播

从右往左的计算方式则是反向传播

局部计算

简单来说就是只用关注当前的简单计算部分，其他复杂的部分不需要管。意思就是计算偏导的那种感觉。

为何用计算图解题

优点：

  1. 局部计算，无论全局是多么复杂，都可以通过局部计算使各个节点致力于简单计算，简化问题。

  2. 可以将中间的计算结果全部保存起来。

  3. 通过反向传播高效计算导数。

基于反向传播的导数的传递

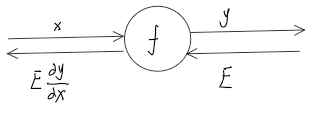
计算图的反向传播

先看一个

的反向传播例子

就是将信号E乘以节点的局部导数，然后传递到下一个节点。如果假设y = x^2 那么导数为2x，那么向下传播的值就是 E*2x，这里的x是正向传递时记录的。

链式法则

就是高数里对复合函数求导。

e.g
令
链式法则和计算图

反向传播

对于每个层，都有forward方法和backward方法，对应正向反向传播。在训练时创建网络时，将每一层存在一个列表当中，顺序正向传播。当需要计算梯度时，将列表翻转，依次执行backward方法进行反向传播，求得梯度。

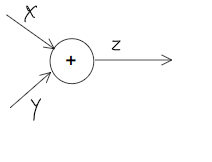
加法节点的反向传播

正向计算图

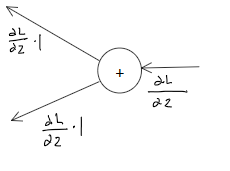
此处是 z = x + y，分别对x，y求偏导。结果都是1。按照前面说的反向传播的话就是将前面给的E乘上局部的导数可知，对于加法来说，都是将E*1传给后面。

python实现：

1
2
3
4
5
6
7
8
9
class AddLayer:
    def __init__(self):
        pass
    def forward(self,x,y):
        return (x + y)
    def backward(self,dout):
        dy = dout * 1
        dx = dout * 1
        return dx,dy

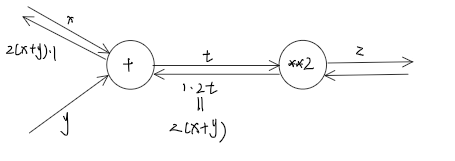
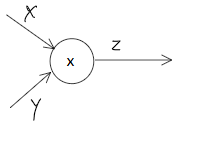
乘法节点的反向传播

考虑 f = xy的导数公式

正向传播图

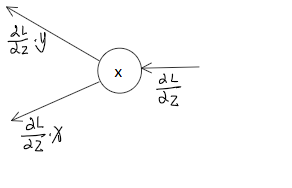
反向传播图

由图中可知对于乘法，是将E乘上输入信号的翻转值。

python实现:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class MulLayer:
    def __init__(self):
        self.x = None
        self.y = None
    
    def forward(self,x,y):
        self.x = x
        self.y = y
        out = x * y
        return out
    def backward(self,dout):
        dx = dout * self.y
        dy = dout * self.x
        return dx,dy

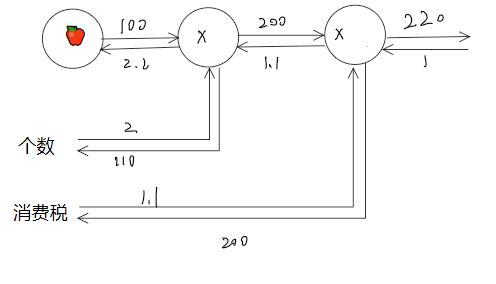
回到苹果的例子

对于买苹果的例子反向传播则是

首先最终结果是220，导数就是1，向后传播，是一个乘法传播，E乘上输入信号的翻转值，也就是200和1.1交换相乘，得到1.1和200。继续向后传播，也是乘法，交换相乘得到2.2和110。

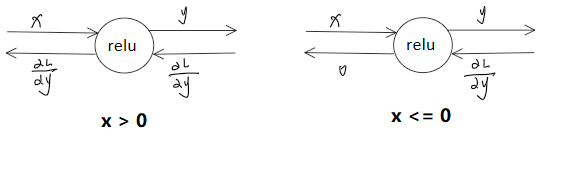
激活函数层实现

ReLU层

数学公式：

求关于x的导数

计算图

python实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Relu:
    def __init__(self):
        self.mask = None
    def forward(self,x):
        self.mask = (x <= 0)
        out = x.copy()
        out[self.mask] = 0
        return out
    
    def backforward(self,dout):
        dout[self.mask] = 0
        dx = dout
        return dx

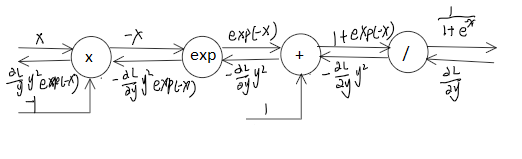
sigmoid层

数学公式

计算图

python实现：

1
2
3
4
5
6
7
8
9
import numpy as np
class sigmoid:
    def __init__(self):
        self.out = None
    def forward(self,x):
        self.out = 1 / (1 + np.exp(-x))
        return self.out
    def backward(self,dout):
        dx = dout * (1.0 - self.out) * self.out

Affine/Softmax 层

Affine层：

就是原先乘上权重加上偏置的操作，对于矩阵的正向反向传播

python实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import numpy as np
class Affine:
    def __init__(self,W,b):
        self.W = W
        self.b = b
        self.x = None
        self.original_x_shape = None
        self.dW = None
        self.db = None
    def forward(self,x):
        self.original_x_shape = x.shape
        x = x.reshape(x.shape[0], -1)
        self.x = x

        out = np.dot(self.x, self.W) + self.b
        return out

    def backforward(self,dout):
        dx = np.dot(dout,self.W.T)
        self.dW = np.dot(self.x.T,dout)
        self.db = np.sum(dout,axis=0)
        dx = dx.reshape(*self.original_x_shape)  # 还原输入数据的形状（对应张量）
        return dx

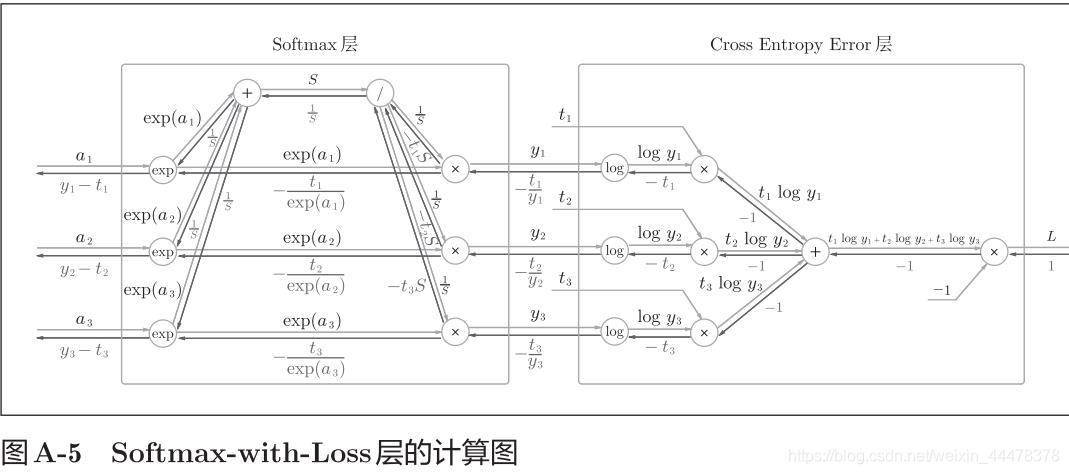
Softmaxwithloss层

python实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
import numpy as np
class SoftmaxWithLoss:
    def __init__(self):
        self.loss = None
        self.y = None
        self.t = None
    def softmax(self,x):
        if x.ndim == 2:
            x = x.T
            x = x - np.max(x, axis=0)
            y = np.exp(x) / np.sum(np.exp(x), axis=0)
            return y.T

        x = x - np.max(x)  # 溢出对策
        return np.exp(x) / np.sum(np.exp(x))

    def cross_entropy_error(self,y, t):
        if y.ndim == 1:
            t = t.reshape(1, t.size)
            y = y.reshape(1, y.size)

        # 监督数据是one-hot-vector的情况下，转换为正确解标签的索引
        if t.size == y.size:
            t = t.argmax(axis=1)

        batch_size = y.shape[0]
        return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
    def forward(self,x,t):
        self.t = t
        self.y = self.softmax(x)
        self.loss = self.cross_entropy_error(self.y,self.t)
        return self.loss
    def backforward(self,dout = 1):
        batch_size = self.t.shape[0]
        if self.t.size == self.y.size:  # 监督数据是one-hot-vector的情况
            dx = (self.y - self.t) / batch_size
        else:
            dx = self.y.copy()
            dx[np.arange(batch_size), self.t] -= 1
            dx = dx / batch_size

        return dx
本作品采用 知识共享署名-相同方式共享 4.0 国际许可协议 进行许可
, ,
最后编辑：2022-02-10