菠萝菠萝卜的博客

深度学习入门笔记02

  • 2021-09-23
  • 作者 菠萝菠萝卜
  • 1302 字
  • 次阅读
  1. 1. 神经网络
    1. 1.1. 一些概念
    2. 1.2. 激活函数
      1. 1.2.1. sigmoid函数
      2. 1.2.2. 阶跃函数
      3. 1.2.3. ReLU函数
      4. 1.2.4. 图形显示
      5. 1.2.5. sigmoid和阶跃函数比较
    3. 1.3. 非线性函数

神经网络

一些概念

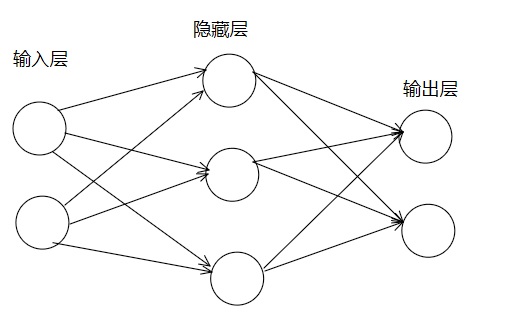
输入层：最左边的一列，用来输入数据的一层

输出层：最右边的一列，用来输出数据

隐藏层：中间层。

神经网络和感知机是相似的，二者最大的区别就在于激活函数。

激活函数

先看一下之前感知机的函数式

简单做下变形

引入一个函数 h(x)，将函数式继续简化

其中

这种会将输入信号的总和转换为输出信号，将这个函数h(x)成为激活函数

sigmoid函数

python实现

1
2
3
import numpy as np
def sigmoid(x):
    return 1.0 / (1.0 + np.exp(-x))

阶跃函数

和之前感知机部分一样，给定一个阈值，当超过阈值就切换输出。这种函数成为阶跃函数

1
2
3
4
import numpy as np
def step_function(x):
    y = x > 0
    return y.astype(np.int)

ReLU函数

ReLU函数：在输入大于0时，直接输出该值；在小于等于0时为0

python实现

1
2
def relu(x):
    return np.maximum(0,x)

图形显示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import numpy as np
import matplotlib.pylab as plt
def step_function(x):
    y = x > 0
    return y.astype(np.int)
def sigmoid(x):
    return 1.0 / (1.0 + np.exp(-x))
def relu(x):
    return np.maximum(0,x)

x = np.arange(-5.0,5.0,0.1)

y = step_function(x)
relu_y = relu(x);
sigmoid_y = sigmoid(x)

plt.plot(x,y,label='step')
plt.plot(x,sigmoid_y,linestyle='--',label='sigmoid')
plt.plot(x,relu_y,linestyle='-.',label='relu')
plt.ylim(-0.1,1.1)
plt.show()

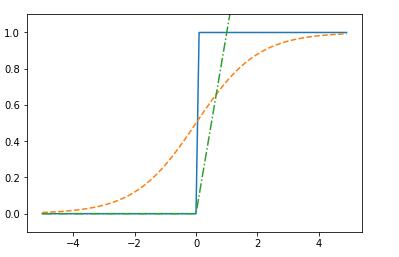
sigmoid和阶跃函数比较

不同点：

​ “平滑性”不同，sigmoid函数是一条平滑的曲线，阶跃函数以0为界，输出发生急剧变化。另一个不同则是，感知机当中神经元之间流动的是0,1的二元信号，而神经网络中流动的是实数信号。

共同点：

​ 二者有相似形状，输入越小，越接近0，输入增大接近1。输出都是在0和1之间。

非线性函数

激活函数都是非线性函数，为啥是非线性函数呢？

举个栗子就能证明出来了，如果激活函数使用了线性函数，h(x) = cx，那么经过三层神经网络， 就变成了 h(h(h(x))) = c c c x，完全相当于 h(x) = c^3 x , 令a = c^3，那和h(x) = a * x 就没区别了，叠加层数变得毫无意义。为了发挥叠加层的优势，需要用非线性函数。

本作品采用 知识共享署名-相同方式共享 4.0 国际许可协议 进行许可
, ,
最后编辑：2022-02-10