感知机

​ 笔记是学习《深度学习入门 基于python理论实践》记录的。由于会一些python基础，所以直接从第二章开始记起。

感知机概念

​ 感知机接收多个输入信号，输出一个信号。

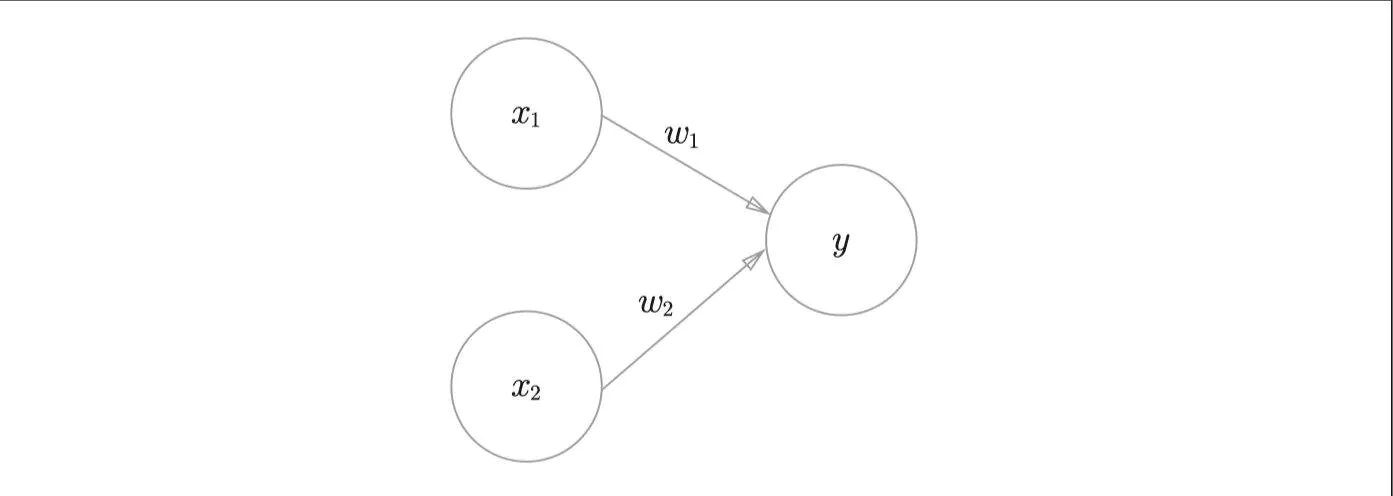
x1,x2是输入信号，w1,w2是权重，y是输出信号。信号送往神经元时，都会乘以相对应的权重(x1w1, x2w2)。神经元计算传来的信号总和，当总和超过一定阈值则输出1，否则输出0。

数学表达：

简单的逻辑电路

与门

通过感知机来表示与门，也就是说需要找到(w1,w2,θ) 相应的权重和偏置，满足条件。如：(0.5,0.5,0.7)满足条件，即 （0.5 x1 + 0.5 x2 <= 0.7 时为0， > 0.7时为1）当然(0.5,0.5,0.8)也可以

python实现

1
2
3
4
5
6
7
8
9
10
11

import numpy as np
def AND(x1,x2):
    w = np.array([0.5,0.5,-0.7])
    x = np.array([x1,x2,1])
    temp = np.sum(w*x)
    if temp <= 0:
        return 0
    else:
        return 1
# x设定为[x1,x2,1]后面加个1，完全是图省事，不加一的话，w也得去掉-0.7. 那么temp = np.sum(w * x) - 0.7。
# 如果有人问为什么是-0.7的话，就是上面的公式把θ换到左边去即可(0.5 * x1 + 0.5 * x2 - 0.7 <= 0 or > 0)

与非门

与非门就是跟与门相反，对应(w1,w2,θ)相反即可。(-0.5,-0.5,-0.7)

python实现

1
2
3
4
5
6
7
8
9

import numpy as np
def NAND(x1,x2):
    w = np.array([-0.5,-0.5,0.7])
    x = np.array([x1,x2,1])
    temp = np.sum(w*x)
    if temp <= 0:
        return 0
    else:
        return 1

或门

这部分书上没有给对应的 (w1,w2,θ) ，我自己算了一个。计算过程就是

• 将x1,x2，作为横竖坐标，并将(0,0),(1,0),(0,1),(1,1)点画到坐标中，每个点Y如果是0，画○，如果是1，画×。
• 得到一幅图像，那么需要找到一条线将×和○分开，这条线假设为 y = kx + b 转到 x1,x2坐标上就是 x2 = kx1 + θ.
• 对应 w2x2 = w1x1 + θ，图中可知这个线必然是 大于0，小于1，故 0 < θ < 1，w1 <= -1 ,将w2除到右边去，因为x2 >= 0 ,可知 w2 < 0。
• 得到条件 0 < θ < 1，w1 <= -1， w2 < 0
• 我设定的值为 (-1,-1,0.5)，但是好像刚好和或门相反，然后将值取反即可(1,1,0.5)

python实现

1
2
3
4
5
6
7
8
9
10

import numpy as np
#或门
def OR(x1,x2):
    w = np.array([1.0,1.0,-0.5])
    x = np.array([x1,x2,1])
    temp = np.sum(w*x)
    if temp <= 0:
        return 0
    else:
        return 1

通过这些代码，就能发现，与门，与非门，或门都是具有相同构造的感知机，他们的区别就在于权重参数的值

多层感知机

异或门

异或门：仅当x1，x2当中的一方为1时才会输出1

对于前面的与门，与非门，或门用一层感知机即可实现

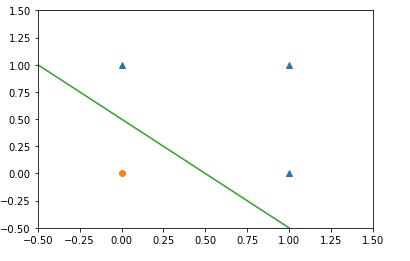
或门感知机可视化。可以发现，与门，与非门，或门都可以用一条线来划分开来。那么异或门

.jpg)

无法用一个感知机划分开。单层感知机无法分离非线性空间。

解决方法： 感知机可以叠加，多层感知机即可完成。

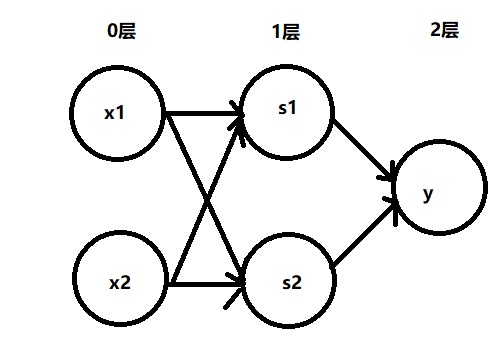
上面x1,x2到s1是做的与非门，到s2是做的或门，s1,s2到y做的是与门。

python实现：

1
2
3
4
5

def XOR(x1,x2):
    s1 = NAND(x1,x2)
    s2 = OR(x1,x2)
    y = AND(s1,s2)
    return y

注意：感知机总共由3层构成，有权重的层只有2层（0层 ~ 1层，1层 ~ 2层），因此称为”2层感知机”。

具体过程：

1. 第0层的两个神经元接收输入信号，并将信号发送至第1层神经元

2. 第1层的神经元将信号发送至第2层神经元，第2层神经元输出y

单层感知机无法表示的东西，通过增加一层就可以解决。